ENSAYOS CON DIPOLOS

ENSAYOS CON DIPOLOS DE ALAMBRES PARA HF

Por: Ing. Ramón Miranda.

YY5RM

Saludos Colegas. En la actualidad y desde los inicios de la radio, para Radioaficionados y usuarios del espectro radioeléctrico en general, las antenas Dipolos construidas con alambres conductores, representan la opción estándar de mayor economía para instalar estaciones de radio en bandas HF. Con el propósito de enriquecer conocimientos adquiridos en cursos de formación y destreza individual, en el presente artículo se describe la teoría básica e información práctica, necesaria para construir y optimizar antenas Dipolos de alambres.

TEMAS

• 1.     Longitud de resonancia y su relación con la corriente, voltaje RF e impedancia, en antenas Dipolos (en este tema se utilizan colores para referir o relacionar estas 4 magnitudes).
• 2.      Técnicas para optimizar Dipolos de longitudes reducidas.
• 3.      Relación de ondas estacionarias (ROE o SWR).
• 4.      Longitud del cable coaxial.
• 5.      Como variar la impedancia del Dipolo.
• 6.      Balun.
• 7.      Medidor de intensidad de campo, tipo RFS.
• 8.      Sugerencias y comentarios finales.

ENSAYOS CON DIPOLOS

LONGITUD RESONANTE DE LA ANTENA DIPOLO DE 1/2 λ

La antena es un dispositivo transductor, que convierte una señal eléctrica, en ondas electromagnéticas (y viceversa) que se propagan en el espacio a una velocidad similar a la de la luz. La longitud de onda (λ) representa la distancia recorrida por una sola onda electromagnética, la cual a su vez determina el tipo de propagación deseada y en especial, las características y dimensiones de las antenas.

Existen longitudes de antenas que mejor se adaptan o acomodan a la λ, las cuales determinan la mejor resistencia de radiación, optima distribución de corriente y máxima eficiencia de dicha antena (longitud resonante de antena).

Por cada brazo de la antena, esta longitud resonante presenta una distribución de corriente, la cual “siempre será de mínima intensidad hacia el extremo donde culminan dichos brazos” y de máxima intensidad en los extremos donde se conectan hacía la línea de transmisión, o directamente al transmisor. Por el contrario, la distribución del voltaje siempre será máximo hacia los extremos, donde culminan los brazos de antena y mínimo voltaje en los extremos que conectan hacia la línea de transmisión. La Dipolo estándar de 1/2 λ, se considera como una antena compuesta de dos tramos o brazos resonantes de 1/4 λ cada uno y de polaridades opuestas.

Típicamente se representa la distribución de corriente y voltaje como en la gráfica anterior (se refieren a las amplitudes de ondas de ambas magnitudes). La gráfica siguiente representaría las amplitudes de ondas, realmente como se verían mediante instrumentos de medición, a lo largo de la antena Dipolo:

La relación entre estos voltajes y corrientes a lo largo del Dipolo estándar de 1/2 λ, determinan impedancia (Z ) mínima en el centro de la misma (aproximadamente 75 Ω para Dipolos horizontales y 50 Ω para forma de V invertida) y máxima hacia los extremos.

Esta impedancia de antena es compleja, es decir, está compuesta de porción real o resistiva (R de la siguiente grafica) y porción imaginaria o reactiva (jX de grafica). Cuando la longitud física de la antena Dipolo es superior de la longitud resonante, entonces incrementa la reactancia inductiva (XL de signo positivo, ó +jX) de su impedancia compleja, si por el contrario, es inferior de la longitud resonante, entonces incrementa la reactancia capacitiva (XC de signo negativo, ó -jX).

La grafica siguiente muestra un análisis virtual realizado mediante el programa MMANA-Gal, donde se simula una antena Dipolo Horizontal HF, calculada para transmitir en 7.1 MHz, montada a 9 metros de altura, la cual determinó resonancia en 7.104 MHz, con una impedancia compleja aproximada de Z = 70.78 –j0.0439 Ω  (nota: cuando jX se aproxima a 0.0 Ω, indica correcta longitud de resonancia).

La longitud resonante de la antena, anula o cancela componentes reactivas (jX = 0.0 Ω) garantizando máxima eficiencia de la misma, debido a que su impedancia compleja es puramente resistiva, por lo tanto absorbe la máxima potencia posible, proveniente desde el transmisor. Cuando la longitud física de la antena, no coincide con la longitud de resonancia, entonces se incrementan las pérdidas a causa de presencia de componentes reactivos en su impedancia compleja (jX ≠ 0.0 Ω). Las imágenes MMANA-Gal siguientes, muestran el ancho de banda, SWR e impedancias de la misma antena Dipolo HF resonante en 7.1 MHz, donde se aprecia que se hace larga (+jX) para frecuencias altas y se hace pequeña (-jX) para frecuencias bajas.

Para antenas Dipolos de 1/2 λ, la longitud de resonancia típicamente se calcula mediante una constante (142.5), la cual se divide entre la frecuencia en Megahertz y el resultado dará en metros. Ejemplo: Para banda de 40 Metros, usando 7.1 MHz como frecuencia central del ancho de banda: 142.5 / 7.1 MHz = 20.07 metros, es decir, la longitud de cada brazo del Dipolo medirá 10.03 metros (1/4 λ cada uno).

Esta longitud de resonancia en antena, es menor en aproximadamente -5% de la 1/2 λ física con cual se propagan las ondas electromagnéticas en el espacio libre y se debe principalmente a la relación longitud/diámetro, chaqueta (envoltura plástica) de los alambres conductores que conforman ambos brazos del Dipolo, a esta reducción de longitud se adicionan otros factores tales como, la proximidad al suelo, el efecto de borde (Endeffect), tipo de metal conductor, etc.

Para el caso de antenas Dipolos en V invertida, la proximidad entre el suelo y los extremos del Dipolo, incrementan la reactancia capacitiva de la impedancia compleja en la antena, haciéndola ver de mayor longitud y desplazando la resonancia hacia otra frecuencia menor, por consiguiente se debe restar hasta aproximadamente un -5% de la longitud calculada, es decir, pudiera calcularse variando la constante desde 135, hasta 142.5 y dividirla entre la frecuencia. Se sugiere que los extremos deben estar lo más separado posible del suelo y conformando un ángulo no menor de 90 grados en el vértice (entre 90° y 120°).

A pesar que la estructura atómica del cobre, permite mejor conducción de corriente eléctrica que el aluminio y que la RF circula por el exterior del metal conductor, en experimento fallido realizado con una Dipolo V invertida, construida con tubos de aluminio, el exceso de reactancias desplazó significativamente la frecuencia de resonancia, produciendo acortamiento excesivo en la longitud de la misma y desmejoramiento considerable en la intensidad de campo.

La imagen siguiente representa la variación de impedancia en el espectro de frecuencias, para una antena Dipolo estándar de 1/2 λ, alimentada en el centro de la misma y calculada para transmitir en 20 MHz. Se aprecia que existen múltiples frecuencias donde la impedancia de dicho Dipolo, adquiere valores máximos y mínimos. A estas frecuencias se les denominan armónicas y equivalen a múltiplos de la frecuencia principal o fundamental, es decir:

·         Primera armónica:  20 MHz x 1 = 20 MHz (frecuencia fundamental).

·         Segunda armónica:  20 MHz x 2 = 40 MHz.

·         Tercera armónica:  20 MHz x 3 = 60 MHz.

·         Cuarta armónica:  20 MHz x 4 = 80 MHz.

·         Quinta armónica:  20 MHz x 5 = 100 MHz.

Indiferentemente de la frecuencia, sea armónica o no, “la distribución de corriente en una antena Dipolo, siempre será mínima hacia ambos extremos de la misma”. Esta condición, siempre determina altas impedancias y altos voltajes hacia dichos extremos del Dipolo y es la principal razón por la cual determinará mínima impedancia y máxima corriente en el centro de la misma, exclusivamente en sus frecuencias armónicas impares, es decir, una antena Dipolo estándar, calculada para transmitir en 20 MHz, también permite transmitir con desequilibrios de impedancias aceptables, en aproximadamente 60 MHz, 100 MHz, 140 MHz, etc.

Empleando los mismos colores anteriores (hasta la 5ta armónica), en la imagen siguiente se aprecian máximas amplitudes de corrientes hacia el centro de una antena Dipolo, exclusivamente en sus frecuencias armónicas impares (primera, tercera y quinta).

Notas importantes:

·        La mayoría de rangos de frecuencias asignados para Radioaficionados, son armónicos.

·    Existen antenas Dipolos en las cuales se desplaza el punto de alimentación, pero manteniendo su misma longitud de resonancia (Dipolos OCF [Off-Center Feed], o simplemente Dipolos Windom ), éstas permiten aprovechar las frecuencias armónicas pares (detallado más adelante).

·       Se usan colores aleatorios en las últimas 2 imágenes.

TÉCNICAS PARA OPTIMIZAR ANTENAS DIPOLOS DE LONGITUDES REDUCIDAS

❶ Es posible optimizar antenas Dipolos de longitudes aleatorias, compensando la longitud de resonancia mediante dispositivos reactivos de signos contrarios (bobinas o capacitores) a sus reactancias propias.

Las bobinas incorporan reactancia inductiva (XL), de signo positivo, ideales para cancelar reactancias negativas en dipolos de longitudes reducidas. Por el contrario, los capacitores incorporan reactancia capacitiva (XC), de signo negativo, ideales para optimizar Dipolos de longitudes alargadas (de poca importancia para el tema).

Aunque estas técnicas no mejoran la eficiencia de la antena, si optimizan el mejor rendimiento posible en ella (acorde a su tamaño), mejorando a su vez la distribución ondas de voltajes y corrientes en el sistema y minimizando posibles riesgos de daños en la etapa final del transmisor.

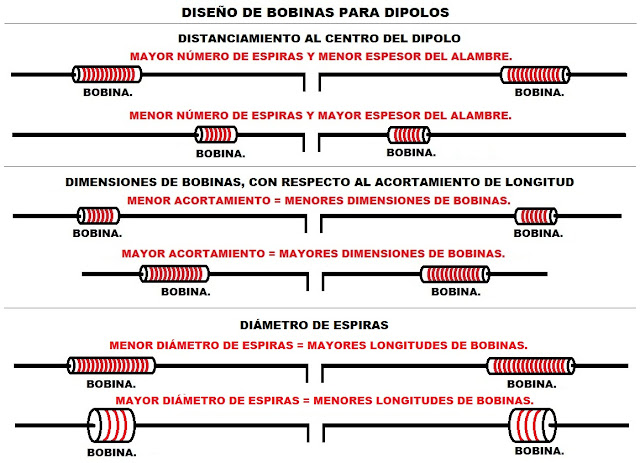
Las características de la bobinas para antenas Dipolos, están determinadas principalmente por la frecuencia y la corriente que circula por ella, seguido por el diámetro, número y separación de espiras, más otras características de poca importancia. Las bajas frecuencias en bandas HF, potencia RF y distanciamiento del centro del Dipolo, hace que se requieran bobinas voluminosas y pesadas.

Cuanto más distanciado del centro del Dipolo se coloquen las bobinas, la baja corriente que circulará por ellas, requieren mayores números de espiras (con alambres de menores espesores) para lograr el mismo efecto reductor de longitud.

Cuanto más reducido sea la longitud del Dipolo, para lograr efecto compensador producido por las bobinas, serán necesarias mayores dimensiones y números de espiras de las mismas.

Mediante bobinas, es posible segmentar las antenas Dipolos multibandas.

En el artículo “BOBINAS PARA DIPOLOS.pdf” se detalla la construcción artesanal de bobinas desarmables y los procedimientos para sintonizar cualquier antena Dipolo de longitud reducida.

En antenas Dipolos Dualband (resonante para dos bandas) estas bobinas suelen colocarse a una distancia del centro del Dipolo, equivalente al 1/4 λ de la frecuencia mayor. Ejemplos:

·         Para bandas 10 y 40 metros (28.5 MHz y 7.1 MHz) = Se colocan aproximadamente a 2,5 metros del centro del Dipolo.

·         Para bandas 15 y 40 metros (21.25 MHz y 7.1 MHz) = Aproximadamente 3.35 metros del centro.

·         Para bandas 20 y 40 metros (14.25 MHz y 7.1 MHz) = Aproximadamente 5 metros del centro.

En el artículo MINIANTENA DIPOLO.pdf, se muestra un ejemplo de construcción y optimización de una Mini Antena Dipolo HF dualband, expandible en tamaño e ideal para adaptarse en cualquier espacio disponible (mínima longitud requerida = 7 metros).

Para lograr mayor ancho de banda en antenas Dipolos Monobandas (ejemplo: Solo para banda de 40 metros, por armónicos, operan en bandas 10, 15 y 20 metros, con pequeñas dificultades), éstas bobinas suelen colocarse cercanas de los extremos del Dipolo, donde la corriente de antena es menor, pero se debe enrollar mayor número de espiras para lograr el mismo efecto reductor de longitud.

En el artículo “ANTENA DIPOLO YY5RM.pdf”, se describen técnicas para optimizar antenas Dipolos OCF de longitudes aleatorias, las cuales logran resonancia modificando el número de espiras en una sola bobina, incorporada a 90 centímetros del extremo del brazo izquierdo de la misma y se acoplan a la línea coaxial mediante balun de relación modificable. Estas permiten adaptarse al máximo del espacio reducido y mal distribuido, logrando excelente equilibrio de impedancias y máxima eficiencia de acorde a su longitud.

❷ Otros procedimientos para optimizar antenas Dipolos de longitudes reducidas, son los sistemas de pliegues (existen diseños de Dipolos totalmente plegadas, con uno y hasta con doble pliegue, como son las Antenas Morgain), adaptadores de carga lineal (consiste en plegar solo el centro de la Dipolo) y adaptadores capacitivos en los extremos del Dipolo (típicamente llamados crucetas o radialitos).

RELACIÓN DE ONDAS ESTACIONARIAS (ROE O SWR)

La relación de ondas estacionarias (ROE o SWR) es una pérdida que afecta el rendimiento del sistema de antena y que pone en riesgo de daños al transmisor.  Es causada por desequilibrios de impedancias entre antena ↔ línea de transmisión, o  línea de transmisión ↔ transmisor. En la actualidad la mayoría de equipos para Radioaficionados son diseñados para cargas de 50 Ω, lo cual, para evitar pérdidas de potencia, las líneas y antenas igualmente deben adaptarse para impedancias de 50 Ω.

Sabiendo que el transmisor tiene una impedancia interna de 50 Ω (Zg), usando línea coaxial de 50 Ω (ZO = impedancia característica), si la antena es de longitud resonante y se corrige totalmente el desequilibrio de impedancias entre dicha antena y la línea coaxial (balun adaptador de impedancias, o similar), entonces tendremos la posibilidad de máxima eficiencia del sistema (correcto modo plano, solo cuando jX = 0 Ω y 1.0 ROE).

Para lograr ROE perfecta, es necesario el uso de costosos y complicados instrumentos de medición denominados “Analizadores de antenas”, los cuales hacen posible discriminar lecturas de las componente resistiva y reactiva de la impedancia compleja, ROE, pérdidas de retorno, coeficiente de reflexión, porcentaje de potencia transmitida, capacitancia, inductancia y otros.

Cuando hay desequilibrio de impedancias, parte de la energía que viaja en un sentido (ondas en sentido hacia la carga o antena = incidentes), es reflejada en sentido contrario (ondas en sentido hacia el generador o transmisor = reflejadas) y viceversa cuando hay desequilibrios en ambos extremos de la línea.

Las interferencias entre ondas incidentes y reflejadas, determinan ondas resultantes de la sumatoria vectorial entre ambas y cuyas relaciones entre amplitudes máximas y amplitudes mínimas, determinan la relación de ondas estacionarias, o simplemente ROE.

Para facilitar el entendimiento, suponiendo que la antena es una carga es resistiva, para calcular la ROE o SWR (entre la antena y la línea), “referencialmente” es posible dividir ambas impedancias, usando la mayor como dividendo y la menor como divisor, ejemplos:  50 Ω / 50 Ω = 1.0 ROE, 75 Ω / 50 Ω = 1.5 ROE, 50 Ω / 25 Ω = 2.0 ROE, 100 Ω / 50 Ω = 2.0 ROE, etc.

1.      Antena = 75 Ω, cable coaxial = 50 Ω.  Cálculo 75 / 50  = 1.5 ROE.

2.      Antena = 150 Ω, cable coaxial = 50 Ω.  Cálculo 150 / 50 = 3.0 ROE.

3.      Antena = 25 Ω, cable coaxial = 50 Ω.  Cálculo 50 / 25 = 2.0 ROE.

4.      Antena =  50 Ω, cable coaxial = 50 Ω.  Cálculo 50 / 50 = 1.0 ROE (excelente equilibrio).

La gráfica siguiente muestra el rendimiento de una antena, respecto a la ROE. Ejemplo: Si la desadaptación de impedancias es 2.0 ROE, el rendimiento de la antena será el 88.9%

LONGITUD DEL CABLE COAXIAL

La RF que se transporta por la línea de transmisión, tiene una velocidad de propagación 60% a 95% menor que a la velocidad de la Luz. Para cualquier impedancia característica de cable coaxial, la longitud de resonancia se calcula usando múltiplos de 1/2 λ y multiplicado por el factor de velocidad de propagación (VP) del mismo cable coaxial.

Ejemplo:  Para la banda de 40 metros, usando 7.1 MHz como frecuencia central del rango y empleando cable coaxial RG8/U con VP de 0.82, el cálculo sería: 150 dividido entre 7.1 y multiplicado por 0.82, el resultado = 17.32 metros ( longitudes correctas: 17.32 metros, 34.64 metros, 51.97 metros, etc.). Esta misma longitud se hace resonante para frecuencias armónicas (frecuencias superiores: bandas de 20, 15, 10, 6 metros), no para frecuencias inferiores (no resonante para bandas de 60, 80 y 160 metros).

Sabiendo que en presencia de ROE (≠ 1.0), la distribución de la corriente y del voltaje RF toman amplitudes diferentes en cada punto a lo largo de la línea coaxial y éstas se repiten a cada 1/2 λ, al usar líneas coaxiales de longitudes aleatorias, mediante sencillos cálculos es posible determinar que este fenómeno afecta la impedancia compleja de la antena, vista desde el extremo de la línea que conecta al transmisor (Zi ), afectando la jX del sistema, la cual a su vez desplaza la ROE y frecuencia de resonancia original de la antena.  Para evitarlo y facilitar el correcto ajuste de la antena Dipolo, se sugiere el uso de longitudes múltiplos de 1/2 λ en la línea coaxial, aunque para cualquier longitud aleatoria en dicha línea, existirá una longitud física en la antena que no es la de resonancia (y viceversa) pero que es capaz de cancelar las componentes reactivas del sistema y a pesar de sus parámetros alterados el sistema se podrá optimizar, pero nunca con su máxima eficiencia.

La siguiente gráfica explicativa muestra un ejemplo de desplazamientos de ROE y frecuencia de resonancia original en una antena CB 11 metros, con resonancia en 27.4 MHz (vista desde el extremo de la línea que conecta al transmisor), donde para este caso se realizan dos recortes en dicha línea coaxial: Es posible observar que en 27.6 MHz, inicialmente la ROE es 1.25, en el 1er recorte el desplazamiento ocasiona un incremento hasta 1.55 ROE y en el 2do recorte incrementa hasta 1.95 ROE.  En los archivos; “Longitud del Cable Coaxial y Nodos.pdf” y “Desplazamiento de la Frecuencia de Resonancia.pdf” se explican estos fenómenos y la importancia del uso de longitudes múltiplos de 1/2 λ en líneas coaxiales.

Para mayor información relacionada con longitudes de la línea coaxial, se sugiere el enlace siguiente:

http://yy5rm.blogspot.com/2011/11/longitud-del-cable-coaxial-y-nodos.html

COMO VARIAR LA IMPEDANCIA DEL DIPOLO

Entre las posibilidades para obtener buen equilibrio de impedancias, podemos variar: ❶ La altura (con respecto al suelo), ❷ El ángulo del vértice (en caso de V invertida), ❸ Desplazar el punto de alimentación, ❹ Variar la longitud,  ❺ Modificar la relación de conversión del balun (no pertenece a la antena. Ver en tema de balun),  ❻ Optar por acoplar con antenatuner (no requiere explicación). Es necesario aclarar cualquier técnica afectará ligeramente la longitud y frecuencia de resonancia.

❶ (Altura) = Las ondas reflejadas por el suelo, al pasar por la antena inducen una corriente de fase diferente a la generada por ella, debilitando o reforzando la corriente total que circula por dicha antena.  Siempre que la altura no supere por lo menos 2 λ (típico en bandas HF, debido al gran tamaño de sus λ), este efecto afectará significativamente la impedancia y longitud de resonancia del Dipolo. En la gráfica siguiente se aprecia que la impedancia del Dipolo (horizontal) tiende a estabilizar sobre las 2 λ de altura y que en aproximadamente cada 1/4 λ (0.25 λ) de altura, se repite la impedancia estándar de la misma:

En la figura M1-3 se muestra el análisis virtual de una antena Dipolo horizontal, calculada para la banda de HF 40 metros, 7.1 MHz, montada a 9 metros de altura. Se observa que al variar dicha altura, desde 2 hasta 15 metros sobre el suelo, la impedancia varía desde 91.78 –j36.51 Ω hasta 7.02 –j37.93 Ω.

❷ (Ángulo del vértice) = Es posible abrir o cerrar el vértice o ángulo conformado entre ambos brazos del Dipolo, hasta obtener mínima lectura de ROE. Se sugieren ángulos entre 90° ↔ 120° visto desde el plano vertical (vista de frente) y entre 120° ↔ 180° vista desde arriba. 

En la figura M1-4 se muestra el análisis virtual de la misma antena Dipolo HF 40 metros, pero en  V invertida y calculada con el vértice a 9 metros de altura (identificada con ② e impedancia = 60.48 –j0.06 Ω), donde se varía el ángulo conformado entre ambos brazos, de manera que ambos extremos queden desde 1 metro (① = 46.96 –j8.93 Ω), hasta 3 metros (③ = 70.96 +j5.12 Ω) de altura sobre el suelo.

La figura M1-5 muestra baja impedancia (7.4 –j66.48 Ω) en la misma antena Dipolo HF 40 metros, 7.1 MHz y conformando ángulo de 30° entre ambos brazos.  Para la simulación es necesario aumentar la altura hasta 11 metros.

❸ (Desplazar el punto de alimentación) = Sabiendo que la impedancia en antenas Dipolos de 1/2 λ es mínima en el centro y máxima hacia los extremos de la misma, es posible desplazar el punto de alimentación (Dipolos OCF) con el propósito de ubicar la impedancia que mejor se adapte al sistema, o a la relación de conversión del balun. Esta técnica también permite adaptar las longitudes de ambos brazos del Dipolo en espacios mal distribuidos, conservando su máxima eficiencia (la longitud y frecuencia de resonancia serán afectadas en la medida que la alimentación se aleje del centro).

Estas antenas Dipolos OCF no dependen de la altura, ángulo del vértice o cualquier otro método similar para lograr excelente equilibrio de impedancias, incluso el 1.0 ROE. La antena Dipolo Windom se alimentan a 1/3 de su longitud total y se acopla hacia la línea coaxial mediante un balun de relación 6:1 (ejemplo: 300 Ω ↔ 50 Ω) y de relación 4:1 (200 Ω ↔ 50 Ω) para antenas Dipolos Windom Carolina, cuya relación de asimetría entre ambos brazos se aproxima al 40% ↔ 60%.

La principal desventaja de Dipolos OCF es la posibilidad de irradiación en la línea, razón por la que se requiere adicionar choques RF para suprimir el problema. Típicamente se emplean ferritas toroidales o enrollando varias espiras del mismo cable coaxial, preferiblemente lo más próximo posible de la antena (también se sugiere separar del mástil o torre del tramo de línea antes del choque RF, debido a que ésta pudiera irradiar energía, igual como si formara parte de la misma antena).

Preferiblemente no alimentar antenas Dipolos OCF a más de 4/5 de su longitud total (aproximadamente entre los puntos #6 y 7 de la figura M8-13), debido a que el comportamiento de su impedancia compleja, corrientes y perdida de resonancia comienzan asemejar con antenas de hilo largo, las cuales se alimentar desde uno de sus extremos, donde las corrientes son mínimas y voltajes RF máximos (máxima impedancia). Generalmente se construyen con longitudes aleatorias (no resonantes) y se acoplan hacia la línea coaxial mediante unun de relación 9:1. Estas antenas de hilo largo son preferidas por aficionados radioescuchas, pero debido a que son antenas de compromiso, su principal desventaja para transmitir RF, es la necesidad de adicionar equipos sintonizadores (en el artículo “ANTENA DE HILO LARGO.pdf “ se adicionan mayores detalles).

❹ (Variar la longitud) = No es lo correcto, pero es el típico procedimiento empleado para optimizar antenas. Consiste en construir el Dipolo a una longitud ligeramente superior de la calculada y en el momento del montaje, recortar pequeños tramos de alambres por igual en ambos extremos de los brazos de dicho Dipolo, hasta obtener mínima lectura de ROE, en la frecuencia deseada. En la figura M8-12 se analiza una antena Dipolo horizontal en una frecuencia fija y su efecto al variar la longitud desde 5.30 hasta 5.08 metros (modifica la ROE, pero la variación de jX indica que se hace resonante para otra frecuencia).

De optar por aplicar este método, es conveniente usar longitudes correctas en la línea coaxial, esto con el propósito de lograr la mejor longitud resonante en la antena y permitir lecturas veraces en los instrumentos de medición.

BALUN

Las principales funciones del balun, como su nombre lo indica, es balancear y corregir la desadaptación de impedancias existente entre la antena Dipolo y la línea de transmisión.

El efecto de balanceador de la antena, consiste en compartir equitativamente la energía proveniente desde la línea de transmisión (o directamente desde el transmisor), entre ambos brazos del Dipolo.

Existen múltiples diseños de balun, con diferentes relaciones de conversión de impedancias (ejemplos:  1:1, 2.25:1, 4:1 y 6:1).

 

Balun especial para antenas Dipolos montadas a baja altura.

Realmente los baluns son transformadores para RF, donde la relación de conversión de impedancias lo determina el cuadrado (N²) de la relación entre el número de espiras de sus dos devanados (primario y secundario), o lo que es inverso, la raíz cuadrada (  ) de la relación entre el número de espiras de sus devanados determina la relación de conversión de impedancias. Ejemplo:

La raíz cuadrada de 4 es 2, por lo tanto, para un balun de relación 4:1, la relación entre el número de espiras de sus devanados es 2 (N = 2), es decir, si tiene 4 espiras en el devanado primario, debe tener 8 espiras en el secundario o viceversa.

La relación entre el número de espiras sus devanados (N), es igual para la relación entre voltajes y corrientes en sus devanados. La potencia es la misma (P =V x I “Sin considerar pérdidas”) en ambos devanados. Ejemplos:

Para un balun de relación 4:1, la transformación de impedancias es cuatro veces (50 Ω ↔ 200 Ω, ó 75 Ω ↔ 300 Ω, etc.), pero la relación entre voltajes y corrientes es dos veces (2:1), es decir, que si duplicamos el voltaje RF, debido a que la potencia debe ser igual en ambos devanados, la corriente debe bajar a la mitad (ejemplo típico para 200 Watts de potencia RF: Si hay 100 voltios con 2 Amperios en devanado de 50 Ω, debe haber 200 voltios con 1 Amperio en el devanado de 200 Ω.

Para un balun de relación 9:1 la transformación de impedancias es nueve veces (50 Ω ↔ 450 Ω, 75 Ω ↔ 675 Ω, etc.), la Raíz Cuadrada es = 3 por lo tanto las relaciones entre el número de espiras, voltajes y corrientes son tres veces (3:1).

Otra de las funciones del balun es balancear un sistema de antena de dos polos irradiantes, con respecto al cable coaxial, evitando posible irradiación en dicha línea (corriente I3).

Para comprobar el correcto balanceo del Dipolo, debajo de cada brazo se debe medir la intensidad de campo (RFS) para comprobar que ambos estén irradiando energía y para el caso de Dipolos alimentados en el centro, es posible comprobar simetría, además de observar cómo responden los cambios en la antena al realizar ajustes (es más efectivo que solicitar reportes de señal).

En el artículo “Balun, Centro de antena y Dipolos.pdf“, se explican técnicas para construcción casera de los mismos, procedimientos para  modificar la relación de conversión de impedancias, construcción del centro de antena para Dipolos y algunos otros detalles.

Existen baluns construidos con cables coaxiales de longitudes específicas, que igualmente balancean y transforman impedancias en antenas Dipolos u otros sistemas. Típicamente de relaciones 1:1 y 4:1:

El balun coaxial de 1/2 λ (180°) produce desfases de ondas, cuyas interferencias o relación entre amplitudes, duplican el voltaje RF y reducen la corriente hasta la mitad, en el punto de alimentación de la antena (acople de impedancias con relación de conversión 4:1), igual como lo haría cualquier transformador para RF o balun bobinado.

El balun coaxial de relación 1:1 no transforma impedancia, consiste en un arnés de 1 λ, donde la línea se conecta a 1/3 λ de éste. La relación entre ondas de voltaje RF y corriente en sus extremos, son similares a los de la entrada.

MEDIDOR DE INTENSIDAD DE CAMPO, TIPO DETECTOR DE RF (RFS)

Los RFS son instrumentos que detectan presencia, e intensidad de señales RF, no requieren conectar al sistema ni trabajar en rango de frecuencias específico (carecen de selectividad), sencillamente se colocan cercano de cualquier antena HF, VHF o UHF y al transmitir, estos mueven la aguja del galvanómetro indicando presencia de RF, generalmente en escala de cero a diez. Esto nos ayuda a saber cuando una antena emite bien, debido a que en oportunidades tenemos buena ROE, pero la antena no emite bien (baja ganancia, campo deformado o mal direccionado para la propagación deseada, etc.).

La mayoría de vatímetros y medidores de ondas estacionarias (ROE o SWR) que tienen una antena y posición “RFS” en el selector, son medidores de intensidad de campo tipo detector y muchos Colegas desconocen su uso.

Cuando se instala una antena en automóvil, con ayuda de estos instrumentos RFS, es posible saber hacia cual dirección del vehículo se emite mejor señal (hacia donde hay mayor intensidad de campo). Igualmente permite optimizar distanciamiento entre elementos de una antena Yagi, para obtener la máxima direccionabilidad y ganancia de la misma (colocando frente a la antena).

En condiciones irregulares del terreno se puede dar un giro de 360° alrededor de la antena, a una distancia constante de ésta, con el propósito de saber hacia dónde está deformado el campo de la antena, o hacia que dirección se obtiene la mayor repuesta.

Al construir Choques para RF o cuando hay algunas pérdidas, es posible apreciar si la línea coaxial irradia energía, o si hay RF en la sala de radios (especialmente al  usar equipos o dispositivos adaptadores en la línea y próximos al radio).

Al ajustar ganma-matchin de Dipolos (Driven), aro de antenas Ringo, recortar o alargar Dipolos, ajustar enfasadores en arreglos colineales de antenas o cualquier otro ajuste similar, típicamente usamos medidor de ROE, pero si complementamos con el RFS, mejora la apreciación de cambios realizados en la antena.

Es posible construir instrumento RFS improvisado, utilizando material de desecho.

SUGERENCIAS Y COMENTARIOS FINALES

¿ QUE LONGITUD DE CABLE COAXIAL DEBERÍA USAR EN HF ?

En Bandas HF, dependiendo de la distancia entre el radio y la antena, preferiblemente usar cables coaxiales cortados a longitudes teóricas (calculada y de ser posible usar instrumento analizador de antenas), construir antenas Dipolos un poco más largas de las longitudes teóricas, para optimizar en el momento del montaje, variando sus longitudes físicas y demás parámetros (ángulo entre brazos, altura, etc.), hasta obtener mínima lectura de ROE. Preferiblemente iniciar los ajustes en la frecuencia más baja del rango deseado y de ser posible complementar con la mayor indicación de RFS alrededor de la antena.

PREPARACIÓN DEL TUBO MÁSTIL PARA LA ESTACIÓN DE RADIOAFICIONADO

 (APROVECHADO AL MÁXIMO)

Todo Radioaficionado desea instalar sus antenas en una torre.  Inicialmente es posible adquirir un tubo mástil de 9 a 15 metros de altura, preferiblemente del tipo telescópico, aunque si desea reducir costos, es posible ensamblarlo con un tubo de 6.6 metros de largo (usado en cercas de alfajol), en el cual se adiciona otro tubo de 3 metros de largo (usado en instalaciones eléctricas tipo EMT). Debido a la diferencia entre ambos diámetros, se deben colocar anillos de material liviano entre ambos tubos.

Para suspender 2 antenas HF de alambres, es posible adicionar una “tee” en el extremo superior del tubo mástil, con el propósito de colocar 2 poleas, lo cual permitiría darle mayor estabilidad a dicho tubo mástil y resistencia a vientos de altas velocidades.  Para minimizar posible inducción de RF hacía los vientos tensores del mástil, que pudieran deformar los diagramas de radiación en ambas antenas HF, es conveniente segmentar la longitud de dichos vientos mediante aisladores:

La fotografía siguiente muestra un ejemplo de mástil aprovechado al máximo.  De optar por esta configuración, en www.qrz.com/db/YY5RM se detalla la construcción casera de cada una de las antenas siguientes:

1.      Dipolo V invertida       = Dualband para 40 y 80 metros.

2.      Dipolo Slooper             =  Plegada o Windom con balun coaxial, para 10 – 15 metros.

3.      Doble Bazooka             = Esta antena opera en amplios rangos de las VHF y UHF.

4.      Yagi VHF 2 metros       = Pudiera ser cualquier antena (altura privilegiada).

5.      Yagi 2.4GHz                   = Usada para internet inalámbrico.

PARA CULMINAR

La intención del presente material, es brindar apoyo didáctico y práctico para Colegas Radioaficionados y técnicos que ensayan con antenas Dipolos de alambres en frecuencias HF.

Los artículos e imágenes que he publicado, son de libre uso, eventualmente son modificados y la última actualización siempre estará disponible para descargar desde www.qrz.com (YY5RM en el buscador), o directamente desde https://www.qrz.com/db/YY5RM .

Atentamente…

…Ramón Miranda.  YY5RM.

Instructor de Electrónica en el Radio Club Venezolano.

Enlaces para descargar el archivo (en formato pdf):
(22-10-2019) = https://documentcloud.adobe.com/link/review?uri=urn:aaid:scds:US:2fdec8b2-8e06-46a4-ad3b-0278f1f2af36
(22-10-2019) = https://www.dropbox.com/s/oah1ngccaovkbq5/ENSAYOS%20CON%20DIPOLOS.pdf?dl=0

Igualmente disponibles y actualizados desde: www.qrz.com/db/YY5RM

                                                                                      Actualizado el 29-12-2018.